電験3種理論の頻出問題、過渡現象ですがその傾向はバラバラです
例として、H13(2001年)~R5上期(2023年上期)までをピックアップしてみました。
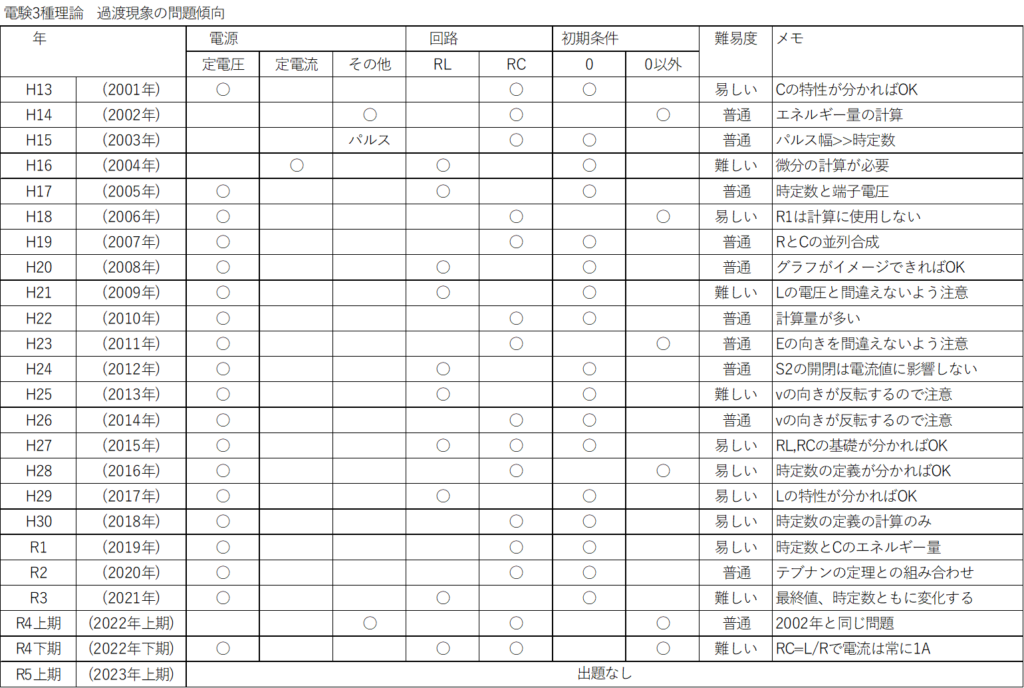
最近は過去問から出題される場合もありますが、基本的には問題傾向の法則は存在せず、原理をしっかりと理解することが必要です。
本項では基本的なRL回路とRC回路について解説します。
①RL回路・・・抵抗(R)、コイル(L)と電源・スイッチで構成された回路
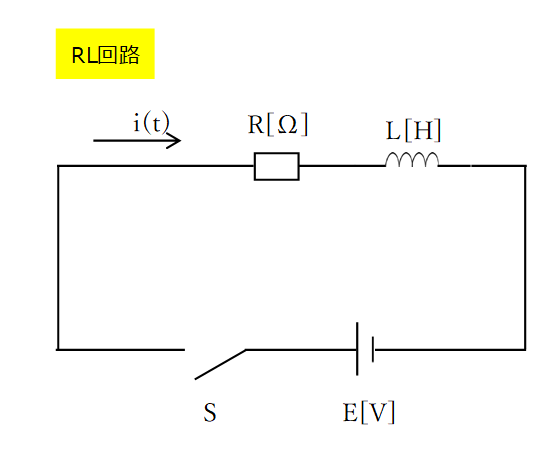
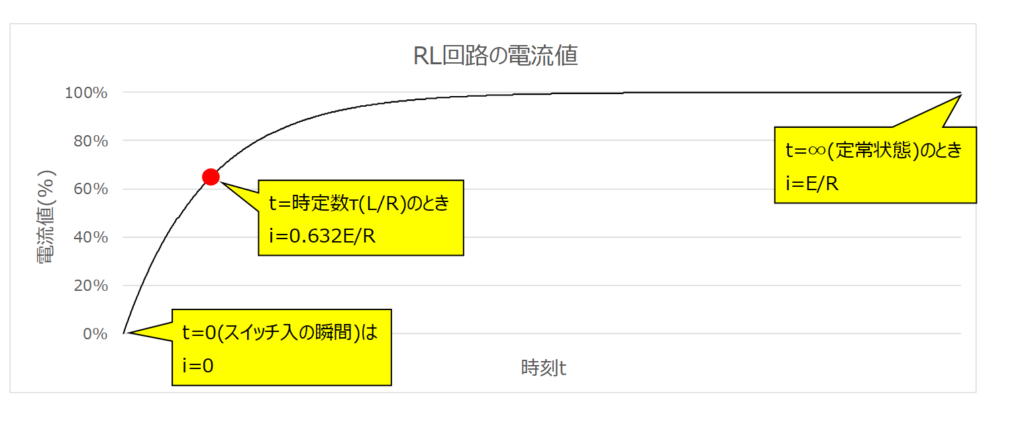
スイッチSを入れたときを\(t=0\)とすると、回路に流れる電流\(i(t)\)は下図の様に変化します。
スイッチ入の瞬間は \(i=0\) ,定常状態のときは \(\displaystyle I=\frac{E}{R}\) になるのが特徴ですね。
②RC回路・・・抵抗(R)、コンデンサ(C)と電源・スイッチで構成された回路
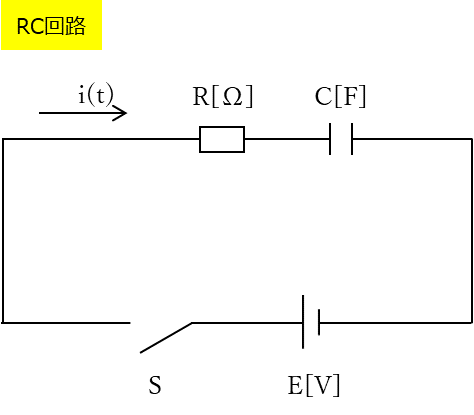
スイッチSを入れたときをt=0とすると、回路に流れる電流\(i(t)\)は下図の様に変化します。
スイッチ入の瞬間は \(\displaystyle I=\frac{E}{R}\) ,定常状態のときは \(i=0\) になるのが特徴ですね。

例題として、H29(2017年)の電験3種理論で出題された過渡現象を解いてみましょう
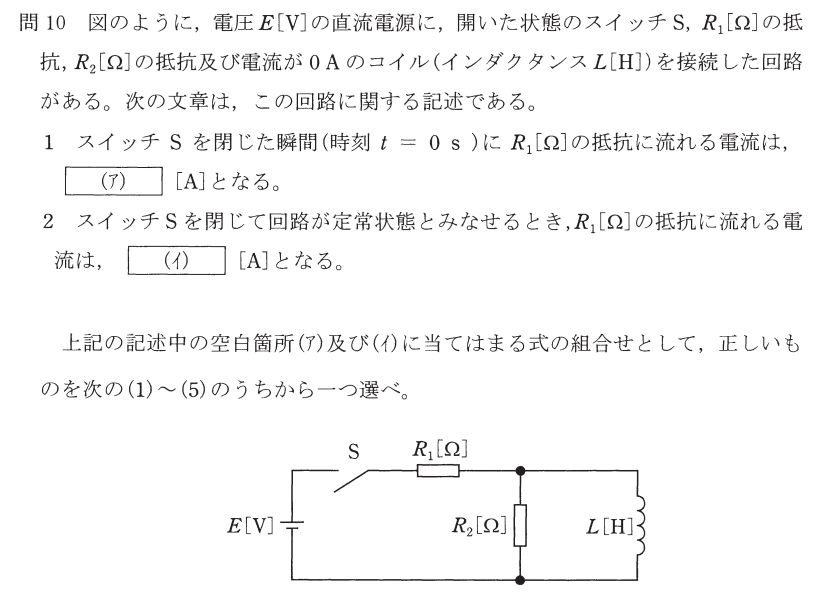

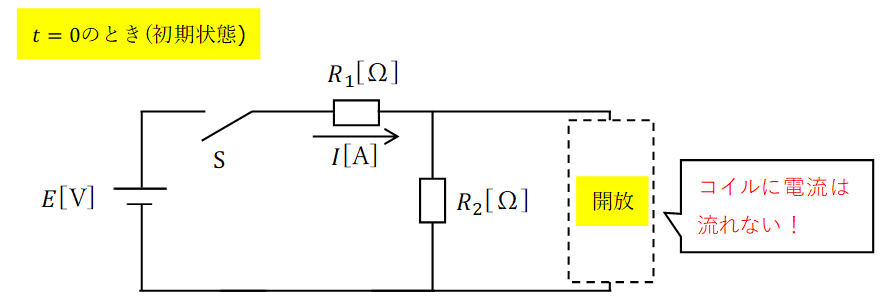
(ア)は\(t=0\)の初期状態について問われています。
スイッチSを閉じた瞬間はコイルLに電流は流れないので、コイルは開放と見なせます
これより、\(\displaystyle I=\frac{E}{R_1+R_2}\)と導くことができます。
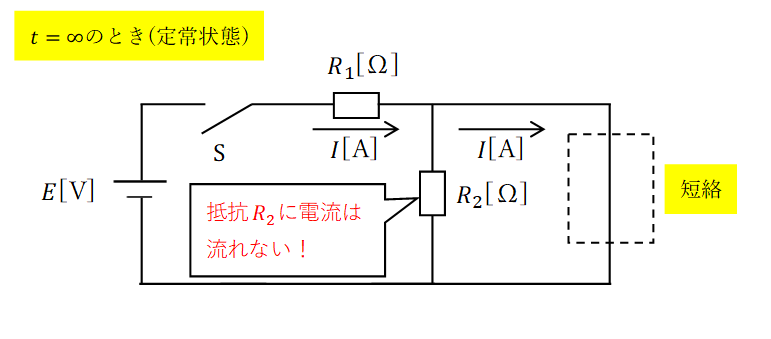
(イ)はスイッチを閉じた後の定常状態について問われています。
定常状態だとコイルは短絡状態と見なせるので、分流の法則より\(R_2\)に電流は流れなくなります。
これより、\(\displaystyle I=\frac{E}{R_1}\)と導くことができます。
上記より答えは(1)となります。
最初はイメージが掴みにくいと思いますが、過去問でいろんなパターンを解くと慣れていきます。
後は時定数も頻出なので覚えておきましょう(将来的に2種以上を狙う場合は微分方程式で導出できるとベストです)
RL回路の時定数・・・\(\displaystyle τ=\frac{L}{R}\)
RC回路の時定数・・・\(\displaystyle τ=RC\)


コメント